swift-algorithm-club
스플레이 트리
스플레이 트리는 구조적으로 균형 이진 탐색 트리와 동일한 데이터 구조다. 스플레이 트리에서 수행되는 모든 연산은 최근에 접근한 값에 빠르게 접근할 수 있도록 재조정을 유발한다. 모든 접근 시, 트리는 재배치되고 접근한 노드는 스플레잉(Splaying)이라 불리는 특정 회전 연산 집합을 통해 트리의 루트로 이동한다.
회전
스플레이(Splaying)를 구성할 수 있는 3가지 회전 타입이 있다:
- ZigZig
- ZigZag
- Zig
노드 a가 루트가 아니고, a가 자식 노드 b를 가지고 있으며, a와 b가 모두 왼쪽 자식이거나 오른쪽 자식인 경우, Zig-Zig 연산을 수행한다.
두 노드 모두 오른쪽 자식인 경우
두 노드 모두 왼쪽 자식인 경우
중요한 점은 ZigZig 연산에서 먼저 중간 노드와 그 부모 노드(조부모 노드)를 회전시키고, 그 후 남은 노드(손자 노드)를 회전시킨다는 것이다. 이렇게 하면 처음에 증가하는 값의 시퀀스를 삽입하여 생성된 경우에도 트리가 균형을 유지할 수 있다(아래 최악의 시나리오와 ZigZig가 왜 먼저 조부모 노드를 회전시키는지에 대한 설명 참조).
노드 a가 루트가 아니고, a에 자식 노드 b가 있으며, b가 a의 왼쪽 자식인데 a가 오른쪽 자식인 경우(또는 그 반대의 경우), Zig-Zag 연산이 수행된다.
대소문자 표기 - 왼쪽에서 오른쪽
좌우 케이스
중요: ZigZag는 먼저 손자 노드를 회전한 후, 그 노드를 새로운 부모와 함께 다시 한 번 회전한다.
Zig
Zig은 회전할 노드 a의 부모가 루트일 때 수행한다.
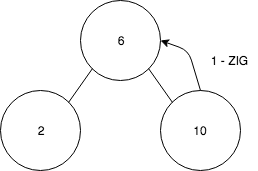
스플레이 연산
스플레이는 특정 연산에 영향을 받은 노드가 트리의 루트가 될 때까지 필요한 만큼 회전을 수행하는 과정이다.
while (node.parent != nil) {
operation(forNode: node).apply(onNode: node)
}
여기서 operation은 적용해야 할 회전을 반환한다.
public static func operation<T>(forNode node: Node<T>) -> SplayOperation {
if let parent = node.parent, let _ = parent.parent {
if (node.isLeftChild && parent.isRightChild) || (node.isRightChild && parent.isLeftChild) {
return .zigZag
}
return .zigZig
}
return .zig
}
적용 단계에서는 알고리즘이 수행할 회전에 따라 관련된 노드를 결정하고, 노드와 그 부모를 재배치한다.
public func apply<T>(onNode node: Node<T>) {
switch self {
case .zigZag:
assert(node.parent != nil && node.parent!.parent != nil, "최소 2개의 상위 노드가 있어야 함")
rotate(child: node, parent: node.parent!)
rotate(child: node, parent: node.parent!)
case .zigZig:
assert(node.parent != nil && node.parent!.parent != nil, "최소 2개의 상위 노드가 있어야 함")
rotate(child: node.parent!, parent: node.parent!.parent!)
rotate(child: node, parent: node.parent!)
case .zig:
assert(node.parent != nil && node.parent!.parent == nil, "루트인 부모 노드가 있어야 함")
rotate(child: node, parent: node.parent!)
}
}
스플레이 트리 연산
삽입
값을 삽입하려면 다음 단계를 따른다:
- 이진 탐색 트리와 동일한 방식으로 값을 삽입한다
- 해당 값을 루트로 스플레이한다
값 삭제
값을 삭제하려면 다음 단계를 따른다:
- 먼저 값을 검색한다. 검색 함수를 실행한 후, 트리에 해당 값이 존재하면 그 값이 새로운 트리의 루트가 된다.
- 트리에 왼쪽 자식만 있는 경우, 왼쪽 자식을 트리의 루트로 변경하고 기존 루트 노드를 제거한다.
- 트리에 오른쪽 자식만 있는 경우, 오른쪽 자식을 트리의 루트로 변경하고 기존 루트 노드를 제거한다.
- 두 자식이 모두 있는 경우, 두 자식의 부모를 nil로 설정해 두 개의 새로운 트리(왼쪽 트리와 오른쪽 트리)로 분리한다.
- 오른쪽 트리의 최소 노드(또는 왼쪽 트리의 최소 노드)를 스플레이(splay)한 후, 왼쪽 트리를 오른쪽 트리의 새로운 루트의 왼쪽 자식으로 설정한다(또는 오른쪽 트리를 왼쪽 트리의 새로운 루트의 오른쪽 자식으로 설정한다). 마지막으로 오른쪽 트리를 반환한다.
탐색
값을 탐색하는 방법:
- 이진 탐색 트리에서 값을 탐색하는 것과 동일한 방식으로 진행한다.
- 값을 포함하는 노드를 찾아 루트로 스플레이한다.
- 값을 찾지 못한 경우, 탐색한 값의 부모 노드가 될 노드를 스플레이한다.
최솟값과 최댓값
- 트리에서 원하는 값을 탐색한다
- 해당 노드를 루트로 스플레이한다
예제
예제 1
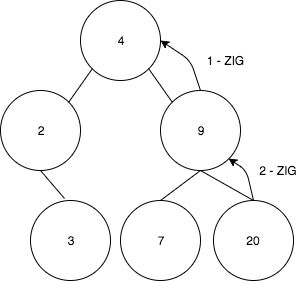
find(20) 연산이 수행되었고, 이제 값 20을 루트로 스플레이해야 한다고 가정해 보자. 이 과정은 다음과 같은 단계로 진행된다:
- 현재 ZigZig 경우에 해당하므로, 9를 4로 회전시킨다.
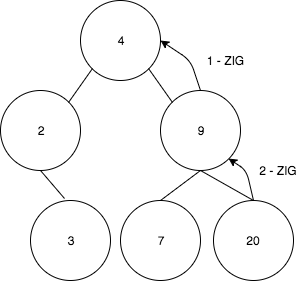
- 첫 번째 회전 후 다음과 같은 트리가 생성된다:
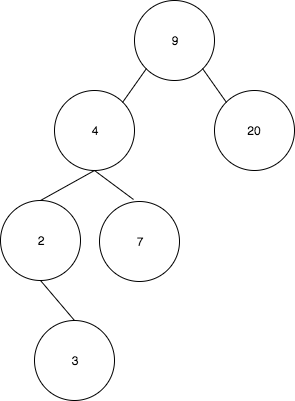
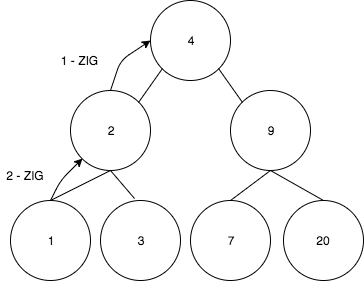
- 마지막으로 20을 9로 회전시킨다.
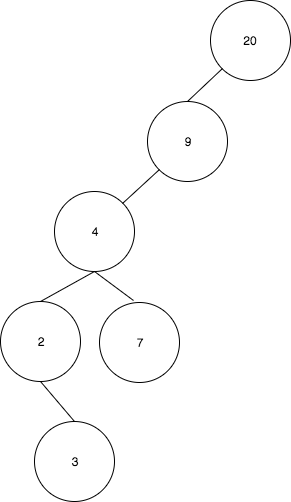
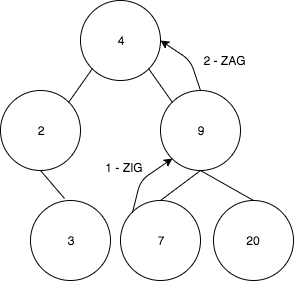
이제 insert(7) 연산이 수행되고, ZigZag 상황에 있다고 가정해 보자.
- 먼저 7을 9로 회전한다.
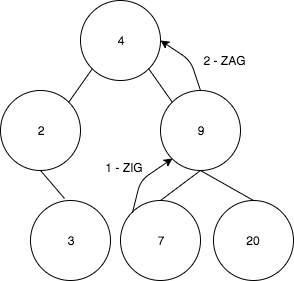
- 결과 트리는 다음과 같다:
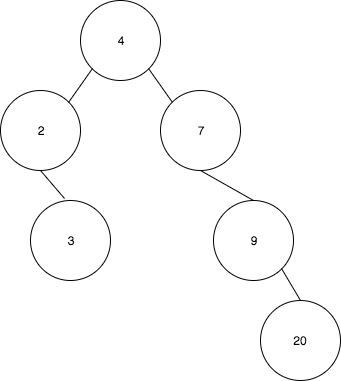
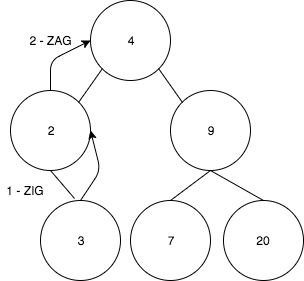
- 마지막으로 7을 4로 회전한다.
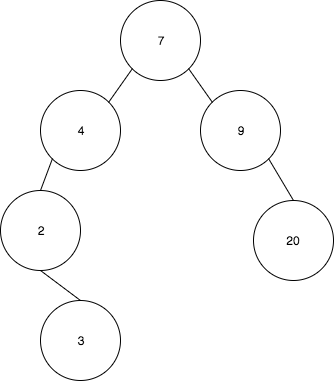
장점
스플레이 트리는 자주 요청되는 요소에 빠르게 접근할 수 있는 효율적인 방법을 제공한다. 이러한 특징 덕분에 캐시나 가비지 컬렉션 알고리즘을 구현하는 데 적합하다. 또한 데이터 집합에서 특정 요소들에 반복적으로 접근해야 하는 문제를 해결할 때도 유용하게 사용할 수 있다.
단점
스플레이 트리는 항상 완벽하게 균형 잡혀 있지 않다. 따라서 트리의 모든 요소를 증가하는 순서로 접근할 경우, 트리의 높이가 n이 된다.
시간 복잡도
| 케이스 | 성능 |
|---|---|
| 평균 | O(log n) |
| 최악 | n |
여기서 n은 트리에 있는 아이템의 수를 나타낸다.
최악의 성능 예시
연속된 값을 Splay Tree에 삽입하는 경우를 가정해 보자. 예를 들어 [1,2,3,4,5,6,7,8]과 같은 수열을 삽입한다고 해보자.
트리 구성 과정은 다음과 같다:
-
숫자 1을 삽입한다.
-
2를 삽입한다.
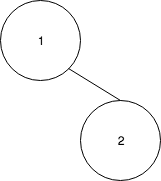
- 2를 루트로 스플레이한다.
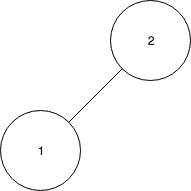
- 3을 삽입한다.
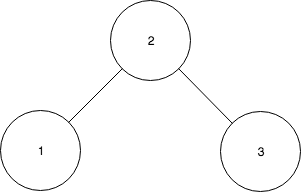
- 3을 루트로 스플레이한다.
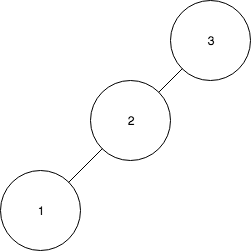
- 4를 삽입한다.
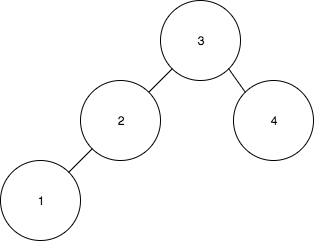
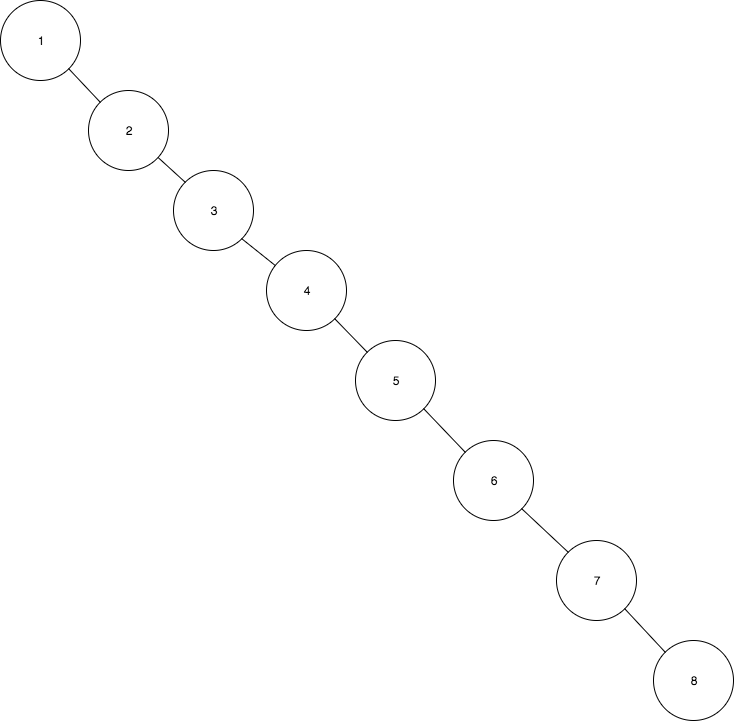
- 나머지 값을 모두 삽입한 후 트리의 모습은 다음과 같다:
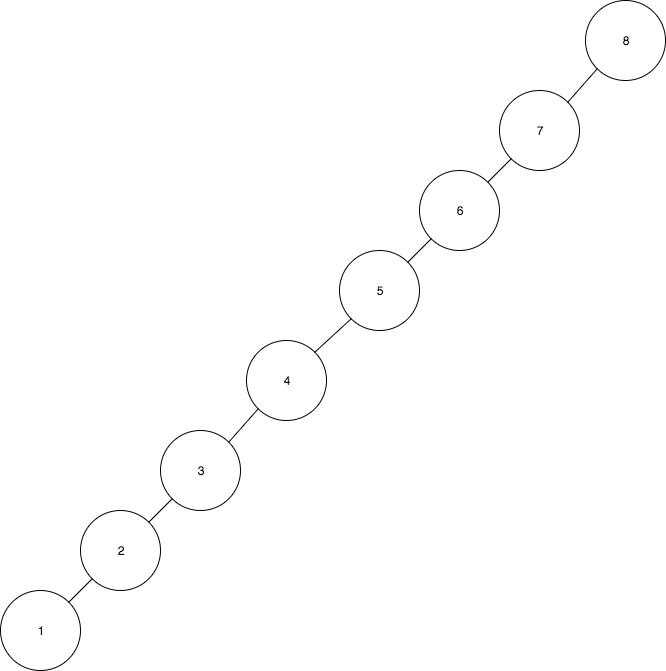
이와 같은 방식으로 계속해서 수열을 삽입하면 트리는 불균형해지고, 삽입된 값의 개수 n만큼의 높이를 가지게 된다. 이렇게 구성된 트리에서 find(1)과 같은 연산을 수행하면 O(n)의 시간이 소요된다.
ZigZig 회전 순서: 조부모 노드 먼저
스플레이 트리의 특성과 find(1) 연산 후 수행되는 ZigZig 회전 덕분에 트리는 다시 균형을 잡는다. 이는 ZigZig 회전 순서를 지켰을 때만 가능하며, 회전은 조부모 노드를 먼저 대상으로 한다.
ZigZig 회전의 순서는 다음과 같다:
- 2를 3으로 회전
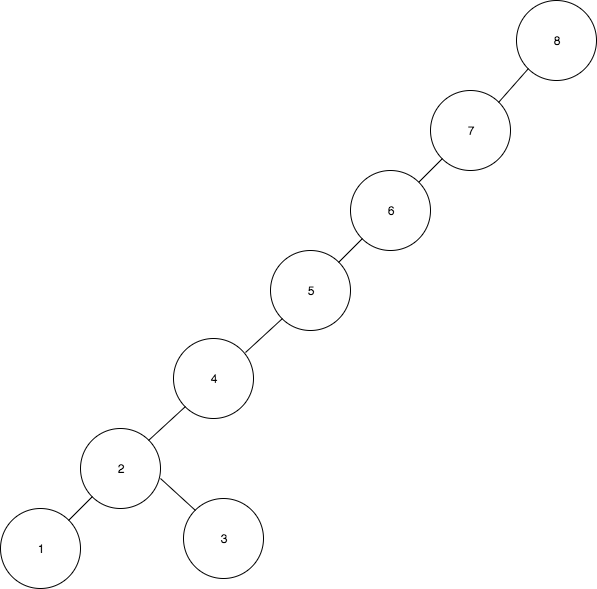
- 1을 2로 회전
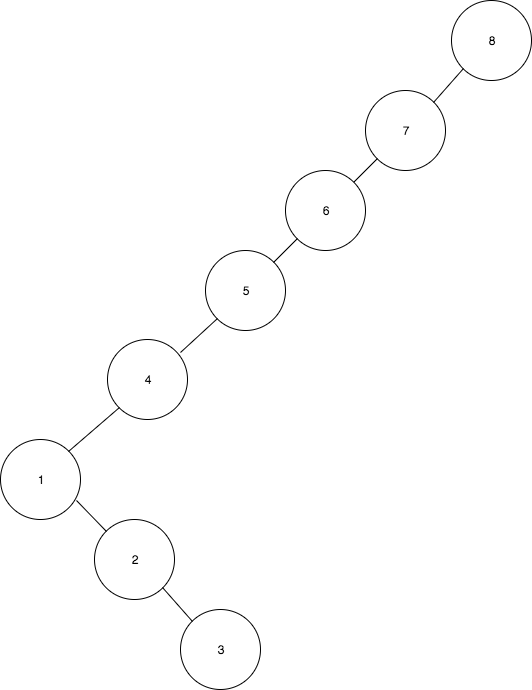
- 4를 5로 회전
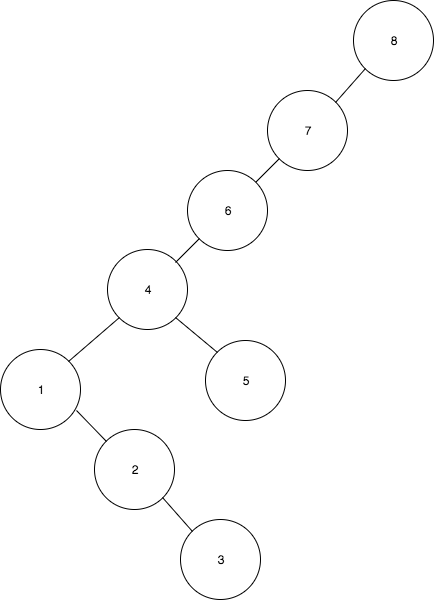
- 1을 4로 회전
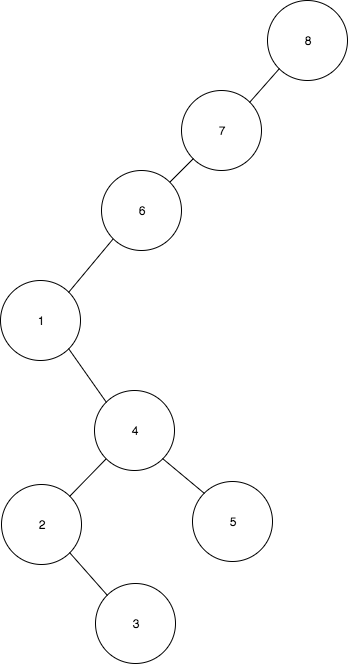
- 마지막으로 1을 루트로 스플레이한 후 트리는 다음과 같이 된다:
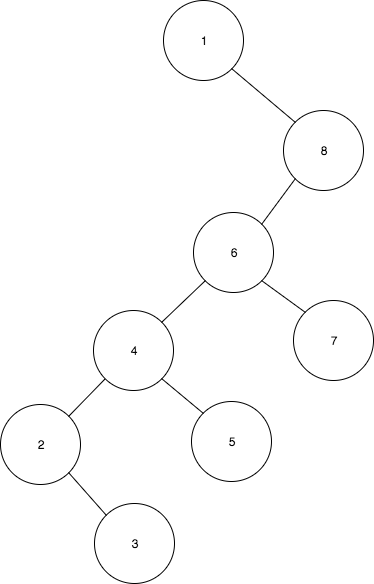
위 예제를 통해 조부모 노드로 먼저 회전하는 것이 왜 중요한지 알 수 있다. 초기 높이가 8이던 트리가 높이 6으로 줄어들었다. 만약 트리가 더 높았다면, 스플레이 연산 후 초기 높이의 거의 절반 정도로 줄어들었을 것이다.
ZigZig 잘못된 회전 순서
회전을 할 때 조부모 노드가 아닌 부모 노드를 먼저 처리했다면, 요소들의 위치만 반대로 바뀌었을 뿐 여전히 균형이 맞지 않는 트리가 만들어졌을 것이다.
함께 보기
캘리포니아 대학교 버클리 캠퍼스 - CS 61B 강의 34: 스플레이 트리
Swift 알고리즘 클럽을 위해 Barbara Martina Rodeker가 작성