최단 경로 (가중치 없는 그래프)
목표: 그래프에서 한 노드에서 다른 노드로 이동하는 최단 경로를 찾는다.
다음과 같은 그래프가 있다고 가정하자:
노드 A에서 노드 F로 가는 최단 경로를 찾고 싶을 수 있다.
그래프가 가중치가 없는 경우, 최단 경로를 찾는 것은 간단하다. 너비 우선 탐색(BFS) 알고리즘을 사용하면 된다. 반면 가중 그래프의 경우에는 다익스트라 알고리즘을 사용할 수 있다.
가중치 없는 그래프: 너비 우선 탐색
너비 우선 탐색은 트리나 그래프 데이터 구조를 탐색하는 방법 중 하나다. 시작 노드에서 출발해 가장 가까운 이웃 노드를 먼저 탐색한 후, 다음 레벨의 이웃 노드로 이동한다. 이 과정에서 시작 노드와 다른 노드 간의 최단 경로를 자동으로 계산할 수 있다.
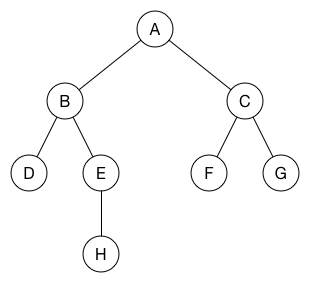
너비 우선 탐색의 결과는 트리로 표현할 수 있다:
트리의 루트는 너비 우선 탐색을 시작한 노드다. 노드 A에서 다른 노드까지의 거리를 찾으려면 트리에서 간선의 수를 세면 된다. 예를 들어 A와 F 사이의 최단 경로는 2다. 이 트리는 경로의 길이뿐만 아니라 A에서 F(또는 다른 노드)로 가는 실제 경로도 알려준다.
이제 너비 우선 탐색을 실제로 적용해 A에서 다른 모든 노드까지의 최단 경로를 계산해 보자. 시작 노드 A를 큐에 추가하고 거리를 0으로 설정한다.
queue.enqueue(element: A)
A.distance = 0이제 큐는 [ A ]다. A를 큐에서 제거하고, 바로 연결된 이웃 노드 B와 C를 큐에 추가한다. 이때 거리는 1로 설정한다.
queue.dequeue() // A
queue.enqueue(element: B)
B.distance = A.distance + 1 // 결과: 1
queue.enqueue(element: C)
C.distance = A.distance + 1 // 결과: 1이제 큐는 [ B, C ]다. B를 큐에서 제거하고, B의 이웃 노드 D와 E를 큐에 추가한다. 이때 거리는 2로 설정한다.
queue.dequeue() // B
queue.enqueue(element: D)
D.distance = B.distance + 1 // 결과: 2
queue.enqueue(element: E)
E.distance = B.distance + 1 // 결과: 2이제 큐는 [ C, D, E ]다. C를 큐에서 제거하고, C의 이웃 노드 F와 G를 큐에 추가한다. 이때 거리도 2로 설정한다.
queue.dequeue() // C
queue.enqueue(element: F)
F.distance = C.distance + 1 // 결과: 2
queue.enqueue(element: G)
G.distance = C.distance + 1 // 결과: 2이 과정은 큐가 비워질 때까지 반복되며, 모든 노드를 방문하게 된다. 새로운 노드를 발견할 때마다 부모 노드의 거리에 1을 더해 거리를 계산한다. 이 과정은 너비 우선 탐색 알고리즘과 동일하지만, 여기서는 이동한 거리도 함께 추적한다.
구현 코드는 다음과 같다:
func breadthFirstSearchShortestPath(graph: Graph, source: Node) -> Graph {
let shortestPathGraph = graph.duplicate()
var queue = Queue<Node>()
let sourceInShortestPathsGraph = shortestPathGraph.findNodeWithLabel(label: source.label)
queue.enqueue(element: sourceInShortestPathsGraph)
sourceInShortestPathsGraph.distance = 0
while let current = queue.dequeue() {
for edge in current.neighbors {
let neighborNode = edge.neighbor
if !neighborNode.hasDistance {
queue.enqueue(element: neighborNode)
neighborNode.distance = current.distance! + 1
}
}
}
return shortestPathGraph
}이 코드를 플레이그라운드에 추가하고 다음과 같이 테스트할 수 있다:
let shortestPathGraph = breadthFirstSearchShortestPath(graph: graph, source: nodeA)
print(shortestPathGraph.nodes)출력 결과는 다음과 같다:
Node(label: a, distance: 0), Node(label: b, distance: 1), Node(label: c, distance: 1),
Node(label: d, distance: 2), Node(label: e, distance: 2), Node(label: f, distance: 2),
Node(label: g, distance: 2), Node(label: h, distance: 3)
참고: 이 버전의
breadthFirstSearchShortestPath()함수는 실제로 트리를 생성하지 않고 거리만 계산한다. 그래프를 트리로 변환하는 방법은 최소 신장 트리를 참고하자.
작성자: Chris Pilcher와 Matthijs Hollemans