그래프

이 주제에 대한 튜토리얼은 여기에서 확인할 수 있다.

그래프는 다음과 같은 모습을 가진다:

컴퓨터 과학에서 그래프는 정점(vertex) 집합과 간선(edge) 집합으로 정의된다. 정점은 원으로 표현되고, 간선은 정점들을 연결하는 선이다. 간선은 하나의 정점을 다른 정점들과 연결한다.

참고: 정점은 때로 "노드(node)"라고 불리며, 간선은 "링크(link)"라고도 한다.

그래프는 소셜 네트워크를 표현할 수 있다. 각 사람은 정점이 되고, 서로 알고 있는 사람들은 간선으로 연결된다. 다음은 역사적으로 다소 부정확한 예시다:

그래프는 다양한 형태와 크기를 가질 수 있다. 간선은 *가중치(weight)*를 가질 수 있는데, 각 간선에 양수나 음수의 숫자 값을 부여한다. 비행기 노선을 표현한 그래프를 생각해 보자. 도시는 정점이 되고, 비행 노선은 간선이 된다. 이때 간선의 가중치는 비행 시간이나 티켓 가격을 나타낼 수 있다.

이 가상의 항공사에서는 샌프란시스코에서 모스크바로 가는 가장 저렴한 경로는 뉴욕을 경유하는 것이다.

간선은 *방향성(directed)*을 가질 수도 있다. 위에서 언급한 예시들은 모두 방향성이 없는 간선을 사용했다. 예를 들어, Ada가 Charles를 알고 있다면, Charles도 Ada를 알고 있다. 반면, 방향성 간선은 단방향 관계를 의미한다. 정점 X에서 정점 Y로의 방향성 간선은 X를 Y에 연결하지만, Y를 X에 연결하지는 않는다.

비행 노선 예시를 이어가자면, 샌프란시스코에서 알래스카의 주노(Juneau)로 가는 방향성 간선은 샌프란시스코에서 주노로 가는 비행편이 있지만, 주노에서 샌프란시스코로 가는 비행편은 없음을 의미한다 (아마 돌아올 때는 걸어야 할 것이다).

다음도 그래프의 예시다:

왼쪽은 트리 구조이고, 오른쪽은 연결 리스트다. 이 둘은 더 단순한 형태의 그래프로 볼 수 있다. 둘 다 정점(노드)과 간선(링크)을 가지고 있다.

첫 번째 그래프는 *사이클(cycle)*을 포함한다. 특정 정점에서 출발해 경로를 따라 이동하다가 다시 원래 정점으로 돌아올 수 있다. 트리는 이런 사이클이 없는 그래프다.

또 다른 일반적인 그래프 유형은 *방향성 비순환 그래프(Directed Acyclic Graph, DAG)*다:

트리와 마찬가지로, 이 그래프는 어떤 사이클도 없다 (어디서 시작하더라도 시작 정점으로 돌아오는 경로가 없다). 하지만 이 그래프는 방향성 간선을 가지며, 반드시 계층 구조를 형성하지는 않는다.

그래프를 사용하는 이유

어떤 이들은 어깨를 으쓱하며 그래프가 대체 왜 중요하냐고 생각할 수 있다. 하지만 그래프는 매우 유용한 데이터 구조다.

데이터를 정점(vertex)과 간선(edge)으로 표현할 수 있는 프로그래밍 문제가 있다면, 이를 그래프로 그려서 너비 우선 탐색이나 깊이 우선 탐색과 같은 잘 알려진 그래프 알고리즘을 사용해 문제를 해결할 수 있다.

예를 들어, 특정 작업이 다른 작업이 끝나야 시작할 수 있는 작업 목록이 있다고 가정해 보자. 이를 비순환 방향 그래프(acyclic directed graph)로 모델링할 수 있다.

각 정점은 작업을 나타낸다. 두 정점 사이의 간선은 목적지 작업이 시작되기 전에 출발지 작업이 완료되어야 함을 의미한다. 예를 들어, 작업 C는 B와 D가 끝나기 전에 시작할 수 없고, B와 D는 A가 끝나기 전에 시작할 수 없다.

이제 문제를 그래프로 표현했으니, 위상 정렬을 수행하기 위해 깊이 우선 탐색을 사용할 수 있다. 이를 통해 작업이 완료될 때까지 기다리는 시간을 최소화하는 최적의 작업 순서를 얻을 수 있다. (여기서 가능한 순서 중 하나는 A, B, D, E, C, F, G, H, I, J, K이다.)

어려운 프로그래밍 문제에 직면할 때마다 스스로에게 물어보라. "이 문제를 그래프로 어떻게 표현할 수 있을까?" 그래프는 데이터 간의 관계를 표현하는 데 초점이 맞춰져 있다. 핵심은 '관계'를 어떻게 정의하느냐에 있다.

음악가라면 이 그래프를 이해할 수 있을 것이다.

정점은 C 메이저 스케일의 코드다. 간선(코드 간의 관계)은 한 코드가 다른 코드를 따를 가능성을 나타낸다. 이는 방향 그래프이므로 화살표의 방향은 한 코드에서 다음 코드로 어떻게 이동할 수 있는지를 보여준다. 또한 가중치 그래프로, 간선의 가중치(여기서는 선의 굵기로 표현됨)는 두 코드 간의 강한 관계를 나타낸다. 보다시피, G7 코드는 C 코드를 따를 가능성이 매우 높고, Am 코드를 따를 가능성은 훨씬 낮다.

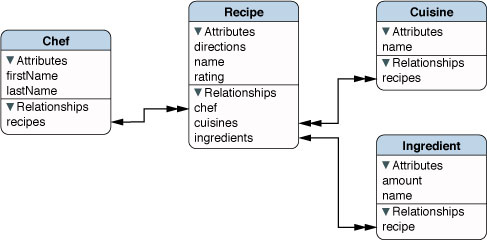
여러분은 이미 그래프를 사용하고 있을지도 모른다. 데이터 모델도 그래프다(Apple의 Core Data 문서에서 발췌).

프로그래머가 사용하는 또 다른 일반적인 그래프는 상태 머신(state machine)이다. 여기서 간선은 상태 간 전환 조건을 나타낸다. 다음은 고양이를 모델링한 상태 머신이다.

그래프는 정말 멋지다. 페이스북은 소셜 그래프를 통해 큰 돈을 벌었다. 데이터 구조를 배울 거라면 반드시 그래프와 다양한 표준 그래프 알고리즘을 선택해야 한다.

정점과 간선, 그래프의 세계!

이론적으로 그래프는 단순히 정점(vertex)과 간선(edge) 객체들의 집합이다. 하지만 이를 코드로 어떻게 표현할까?

주로 두 가지 전략이 있다: 인접 리스트(adjacency list)와 인접 행렬(adjacency matrix).

인접 리스트. 인접 리스트 구현에서는 각 정점이 해당 정점에서 시작하는 간선들의 리스트를 저장한다. 예를 들어, 정점 A가 정점 B, C, D로 향하는 간선을 가진다면, 정점 A는 3개의 간선을 포함하는 리스트를 갖게 된다.

인접 리스트는 나가는 간선(outgoing edges)을 설명한다. A는 B로 향하는 간선을 가지지만, B는 A로 향하는 간선을 가지지 않는다. 따라서 A는 B의 인접 리스트에 나타나지 않는다. 두 정점 사이의 간선이나 가중치를 찾는 작업은 비용이 많이 들 수 있다. 간선에 대한 랜덤 접근이 불가능하기 때문에, 해당 간선을 찾을 때까지 인접 리스트를 순회해야 한다.

인접 행렬. 인접 행렬 구현에서는 정점들을 행과 열로 표현한 행렬이 사용된다. 이 행렬은 정점들이 연결되어 있는지, 그리고 어떤 가중치로 연결되어 있는지를 나타낸다. 예를 들어, 정점 A에서 정점 B로 향하는 가중치 5.6의 방향성 간선이 있다면, 행렬에서 정점 A에 해당하는 행과 정점 B에 해당하는 열의 값은 5.6이 된다.

그래프에 새로운 정점을 추가하는 작업은 비용이 많이 든다. 새로운 행/열을 수용할 수 있는 충분한 공간을 가진 새로운 행렬 구조를 생성하고, 기존 구조를 새로운 구조로 복사해야 하기 때문이다.

그렇다면 어떤 방식을 사용해야 할까? 대부분의 경우 인접 리스트가 적합한 접근 방식이다. 다음은 두 방식의 상세한 비교이다.

V를 그래프의 정점 수, E를 간선 수라고 할 때, 다음과 같은 비교표를 얻을 수 있다:

작업	인접 리스트	인접 행렬
저장 공간	O(V + E)	O(V^2)
정점 추가	O(1)	O(V^2)
간선 추가	O(1)	O(1)
인접 여부 확인	O(V)	O(1)

"인접 여부 확인"이란 특정 정점이 다른 정점과 바로 연결되어 있는지 확인하는 작업을 의미한다. 인접 리스트에서 인접 여부를 확인하는 시간은 **O(V)**이다. 최악의 경우 하나의 정점이 모든 다른 정점과 연결되어 있을 수 있기 때문이다.

희소 그래프(sparse graph)의 경우, 각 정점이 소수의 다른 정점과만 연결되어 있다면, 인접 리스트가 간선을 저장하는 가장 효율적인 방법이다. 반면 밀집 그래프(dense graph)의 경우, 각 정점이 대부분의 다른 정점과 연결되어 있다면, 인접 행렬이 더 적합하다.

다음은 인접 리스트와 인접 행렬의 샘플 구현이다:

코드: 엣지와 버텍스

각 버텍스의 인접 리스트는 Edge 객체로 구성된다:

public struct Edge<T>: Equatable where T: Equatable, T: Hashable {

  public let from: Vertex<T>
  public let to: Vertex<T>

  public let weight: Double?

}

이 구조체는 "출발" 버텍스와 "도착" 버텍스, 그리고 가중치 값을 설명한다. Edge 객체는 항상 방향성을 가지며, 단방향 연결을 나타낸다(위 그림에서 화살표로 표시됨). 무방향 연결을 원한다면, 반대 방향으로도 Edge 객체를 추가해야 한다. 각 Edge는 선택적으로 가중치를 저장할 수 있으므로, 가중치가 있는 그래프와 없는 그래프 모두를 설명할 수 있다.

Vertex는 다음과 같이 정의된다:

public struct Vertex<T>: Equatable where T: Equatable, T: Hashable {

  public var data: T
  public let index: Int

}

이 구조체는 Hashable과 Equatable을 준수하는 제네릭 타입 T로 임의의 데이터를 저장한다. 버텍스 자체도 Equatable을 준수한다.

그래프 구현 코드

참고: 그래프를 구현하는 방법은 다양하다. 여기서 제공하는 코드는 단순히 하나의 예시일 뿐이다. 여러분은 각 문제에 맞게 그래프 코드를 수정해야 할 수도 있다. 예를 들어, 엣지에 weight 속성이 필요하지 않을 수도 있고, 방향성이 있는 엣지와 없는 엣지를 구분할 필요가 없을 수도 있다.

다음은 간단한 그래프의 예시이다:

이 그래프는 인접 행렬(adjacency matrix)이나 인접 리스트(adjacency list)로 표현할 수 있다. 두 개념을 구현한 클래스는 모두 AbstractGraph에서 공통 API를 상속받으므로, 동일한 방식으로 생성할 수 있다. 내부적으로는 각각 다른 최적화된 데이터 구조를 사용한다.

예제 그래프를 저장하기 위해 각 표현 방식을 사용해 방향성과 가중치가 있는 그래프를 만들어 보자:

for graph in [AdjacencyMatrixGraph<Int>(), AdjacencyListGraph<Int>()] {

  let v1 = graph.createVertex(1)
  let v2 = graph.createVertex(2)
  let v3 = graph.createVertex(3)
  let v4 = graph.createVertex(4)
  let v5 = graph.createVertex(5)

  graph.addDirectedEdge(v1, to: v2, withWeight: 1.0)
  graph.addDirectedEdge(v2, to: v3, withWeight: 1.0)
  graph.addDirectedEdge(v3, to: v4, withWeight: 4.5)
  graph.addDirectedEdge(v4, to: v1, withWeight: 2.8)
  graph.addDirectedEdge(v2, to: v5, withWeight: 3.2)

}

앞서 언급했듯이, 방향성이 없는 엣지를 만들려면 두 개의 방향성 엣지를 추가해야 한다. 방향성이 없는 그래프의 경우 다음 메서드를 대신 사용한다:

  graph.addUndirectedEdge(v1, to: v2, withWeight: 1.0)
  graph.addUndirectedEdge(v2, to: v3, withWeight: 1.0)
  graph.addUndirectedEdge(v3, to: v4, withWeight: 4.5)
  graph.addUndirectedEdge(v4, to: v1, withWeight: 2.8)
  graph.addUndirectedEdge(v2, to: v5, withWeight: 3.2)

가중치가 없는 그래프를 만들려면 withWeight 매개변수에 nil을 전달하면 된다.

코드: 인접 리스트

인접 리스트를 유지하기 위해, 정점에 대한 간선 리스트를 매핑하는 클래스가 있다. 그래프는 단순히 이러한 객체의 배열을 유지하고 필요에 따라 수정한다.

private class EdgeList<T> where T: Equatable, T: Hashable {

  var vertex: Vertex<T>
  var edges: [Edge<T>]? = nil

  init(vertex: Vertex<T>) {
    self.vertex = vertex
  }

  func addEdge(_ edge: Edge<T>) {
    edges?.append(edge)
  }

}

이 클래스는 구조체가 아닌 클래스로 구현되어 있다. 따라서 참조를 통해 직접 수정할 수 있다. 예를 들어, 새로운 정점에 간선을 추가할 때 소스 정점이 이미 간선 리스트를 가지고 있는 경우처럼 말이다.

open override func createVertex(_ data: T) -> Vertex<T> {
  // 정점이 이미 존재하는지 확인
  let matchingVertices = vertices.filter() { vertex in
    return vertex.data == data
  }

  if matchingVertices.count > 0 {
    return matchingVertices.last!
  }

  // 정점이 존재하지 않으면 새로운 정점 생성
  let vertex = Vertex(data: data, index: adjacencyList.count)
  adjacencyList.append(EdgeList(vertex: vertex))
  return vertex
}

예제의 인접 리스트는 다음과 같다.

v1 -> [(v2: 1.0)]
v2 -> [(v3: 1.0), (v5: 3.2)]
v3 -> [(v4: 4.5)]
v4 -> [(v1: 2.8)]

여기서 일반적인 형태인 a -> [(b: w), ...]는 a에서 b로 가중치 w를 가진 간선이 존재함을 의미한다. (또한 a에서 다른 정점으로 연결되는 더 많은 간선이 있을 수 있다.)

코드: 인접 행렬

인접 행렬은 2차원 [[Double?]] 배열로 관리한다. nil 값은 간선이 없음을 나타내고, 다른 값은 해당 가중치의 간선이 있음을 의미한다. adjacencyMatrix[i][j]가 nil이 아니면, 정점 i에서 정점 j로 향하는 간선이 존재한다.

정점을 사용해 행렬에 접근하기 위해 Vertex의 index 프로퍼티를 활용한다. 이 프로퍼티는 그래프 객체를 통해 정점을 생성할 때 할당된다. 새로운 정점을 생성할 때 그래프는 행렬의 크기를 조정해야 한다:

open override func createVertex(_ data: T) -> Vertex<T> {
  // 정점이 이미 존재하는지 확인
  let matchingVertices = vertices.filter() { vertex in
    return vertex.data == data
  }

  if matchingVertices.count > 0 {
    return matchingVertices.last!
  }

  // 정점이 존재하지 않으면 새로 생성
  let vertex = Vertex(data: data, index: adjacencyMatrix.count)

  // 기존 행을 오른쪽으로 한 칸 확장
  for i in 0 ..< adjacencyMatrix.count {
    adjacencyMatrix[i].append(nil)
  }

  // 맨 아래에 새로운 행 추가
  let newRow = [Double?](repeating: nil, count: adjacencyMatrix.count + 1)
  adjacencyMatrix.append(newRow)

  _vertices.append(vertex)

  return vertex
}

이렇게 하면 인접 행렬은 다음과 같은 형태가 된다:

[[nil, 1.0, nil, nil, nil]    v1
 [nil, nil, 1.0, nil, 3.2]    v2
 [nil, nil, nil, 4.5, nil]    v3
 [2.8, nil, nil, nil, nil]    v4
 [nil, nil, nil, nil, nil]]   v5

  v1   v2   v3   v4   v5